Optimising portfolio design in a risk / return framework has challenged industry and academics for many decades. Incorporating impact into this framework creates additional dimensionality, significantly increasing the complexity of the portfolio design challenge. This article explores the technical challenge of navigating the 3-D investment framework.
A primer on modern portfolio theory – the 2-D challenge
The foundation of modern portfolio theory is the work of Nobel prize winners Harry Markowitz, James Tobin, and Bill Sharpe. There are various interpretations of the framework, and sometimes it is unfairly criticised. Markowitz sets out a framework for creating an efficient (mean-variance) frontier of portfolio opportunities. Tobin and Sharpe extend on this foundation to demonstrate how to improve risk / return efficiency by blending cash or leverage with the portfolio which has maximum (expected) excess return relative to variance (the ‘market portfolio’).
There are many challenges to modern portfolio theory. These range from the subjectivity of inputs, return distributions for different investments, the way that different investments blend, and liquidity. The broad takeout: be efficient with risk when seeking return.
Interestingly some institutional investors are better placed to efficiently manage the risk / return trade-off.
Pension fund leverage is one example: Australia’s superannuation funds are restricted from applying portfolio leverage directly whereas pension funds in the US, Canada and parts of Europe have fewer restrictions and have incorporated leverage into their portfolios.
Incorporating a third dimension: impact
Accounting for impact creates a fascinating, but complex challenge. Impact represents a third dimension in the portfolio decision framework. To enable us to explore this framework we make two important assumptions:
1. That sustainability and ESG can be aggregated into a single variable: impact.
2. That impact can be measured in a continuous manner (i.e. there is an infinite, not a discrete set, of impact measurements).
A third portfolio variable introduces significant complexity. Where there was one trade-off to consider (return versus risk) there are now three: return versus risk, return versus impact, and risk versus impact. Instead of searching for the optimal portfolio on a two-dimensional risk / return frontier, there is now a three-dimensional risk / return / impact surface on which to locate the optimal portfolio. We illustrate this in Figure 1.
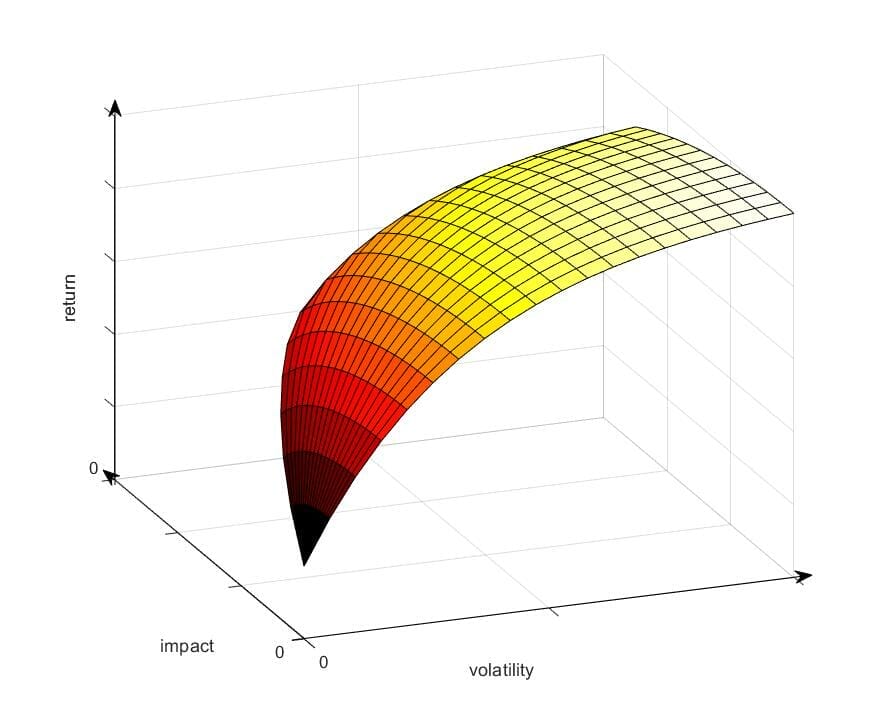
Figure 1: A three-dimensional risk (volatility) / return / impact surface.
Based on Figure 1 we make some important observations:
1. Higher risk, measured by volatility in our simplified framework, can be applied to increasing expected returns and impact (or both).
2. We entertain the possibility that there is a trade-off between impact and return.
3. If we ignore impact the framework collapses down into the familiar modern portfolio theory efficient frontier.
4. For every degree of impact there exists a risk / return frontier.
Accounting for active ownership and engagement
The opportunity for active ownership and engagement activities to improve impact with no effect on returns is topical (here and here). We model the commitment to universal investor activities as incurring a fixed cost (establishing a team, systems etc.) and delivering a fixed expected benefit. Hence the outcome is a fixed uplift in impact.
This is reflected in Figure 2.
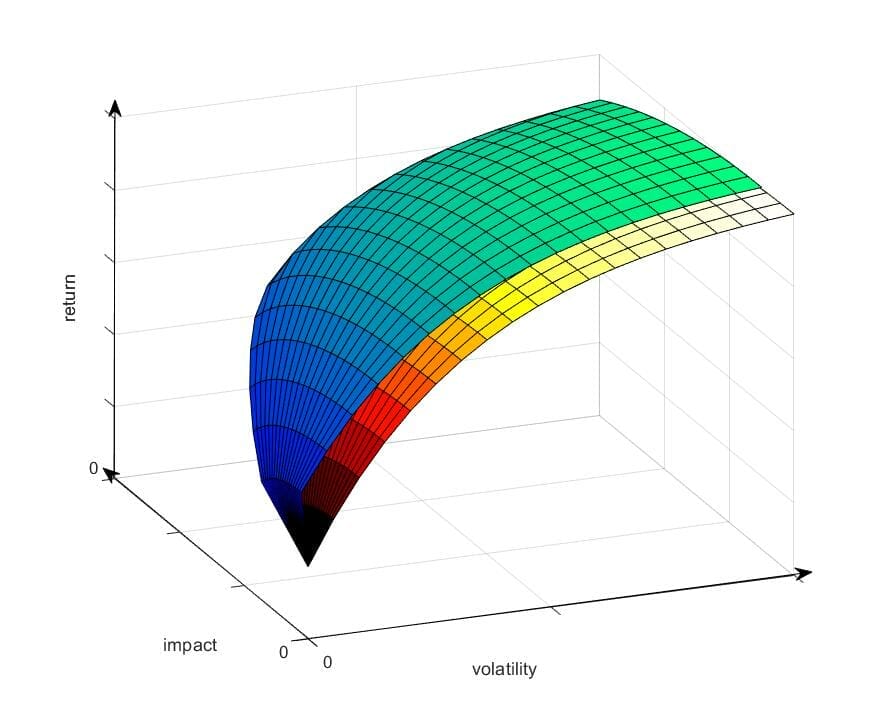
Figure 2: Illustrating the effect of undertaking a program of active ownership and engagement activities.
Figure 2 depicts two surfaces. The first (shaded yellow / red) carries over from Figure 1. The second (green / blue) sits further along the impact axis by the degree of expected net impact from undertaking a program of active ownership and engagement activities.
Identifying the optimal portfolio
Identifying the optimal solution becomes more difficult as more dimensions are added to any problem (econometrician John Rust famously described this as the “curse of dimensionality”).
For academics, utility functions remain the cornerstone for setting objectives, aided by ever-increasing computing power. Utility functions appear to be less applied in industry, perhaps because of their complexity.
A utility function assesses the distribution of possible portfolio outcomes. In doing so it implicitly establishes trade-offs between different dimensions. While traditionally the dimensions have been risk and return, the utility function approach has the capability to provide objectivity when faced with the 3-D challenge created by the incorporation of impact. Note that the trade-offs are not necessarily linear. The exercise of exploring and formalising these trade-offs would make for a wonderful learning experience for pension fund boards.
Two alternative approaches are more likely to be applied, at least in the near-term, as industry adopts 3-D investment frameworks.
Approach 1: Targeted impact
The first approach is to target a specific degree of impact. This effectively converts the 3-D surface back to a single 2-D investment frontier (the thick black line), detailed in Figure 3. This returns the portfolio decision to the familiar 2-D investment frontier problem.
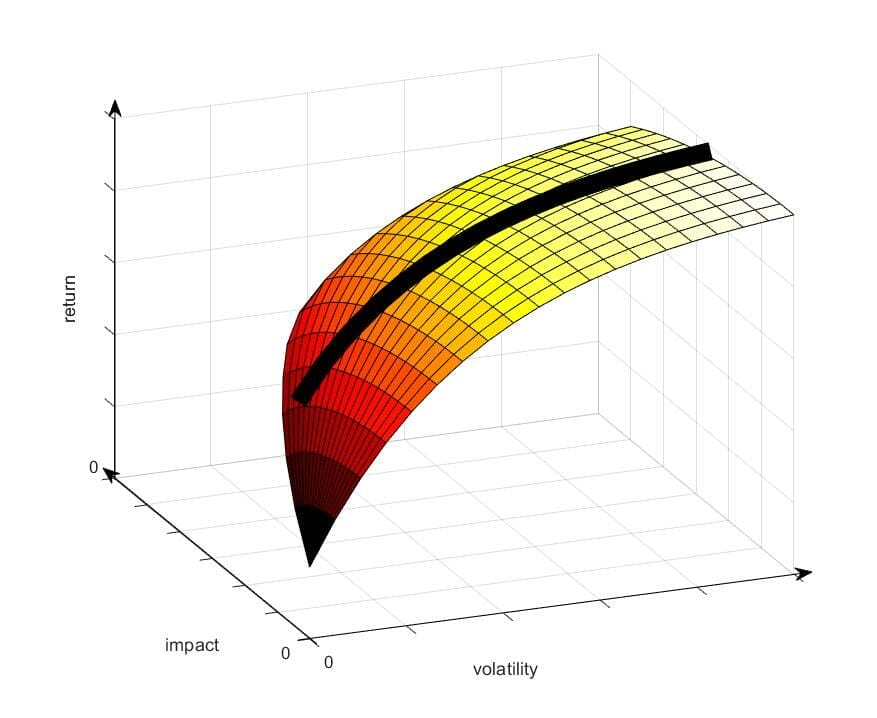
Figure 3: Targeting a fixed degree of impact creates a single risk / return frontier.
Approach 2: Minimum impact threshold
The second alternative approach is to set a minimum impact threshold. This effectively divides the 3-D surface into two segments, both 3-D. In Figure 4 portfolios on the yellow / red surface fail to meet a minimum impact threshold, while portfolio managers are free to search the blue / green surface for the best portfolio outcome.
The advantage of this approach compared to Approach 1 is that it allows portfolio managers to further explore the trade-off between impact and return. For instance further impact may have been attainable, beyond the fixed threshold applied in Approach 1, with little impairment of returns.
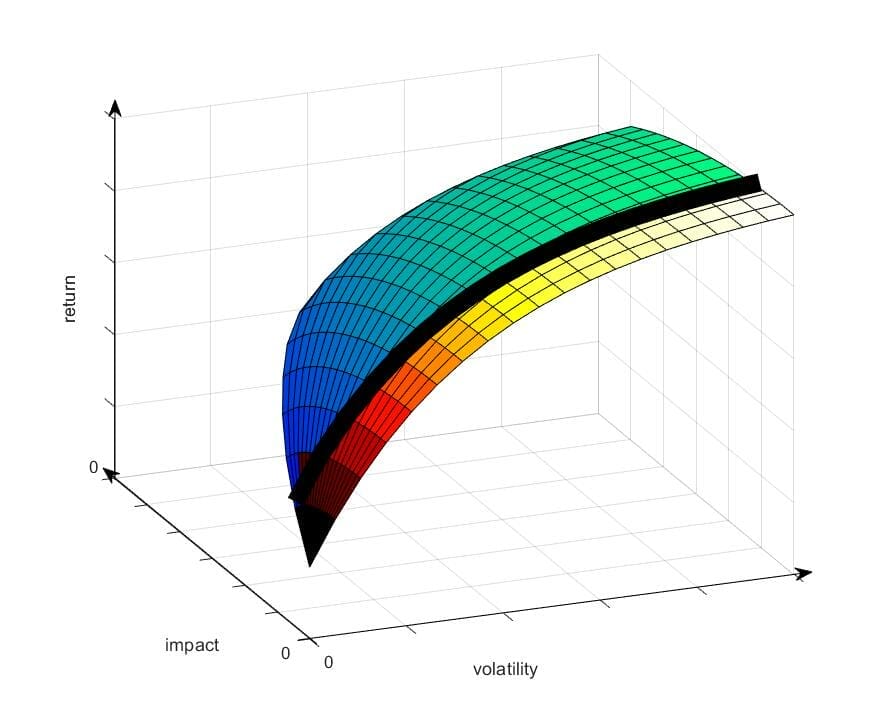
Figure 4: Establishing a minimum impact threshold divides the 3-dimensional risk / return / impact surface into two segments.
Challenges in practice
There are significant in-practice challenges to 3-D investing, which exist over and above the known difficulties of 2-D investing (forecasting return, risk etc.). These include:
- Measuring impact, where the availability of many different datasets creates confusion. A particularly difficult component is the challenge of integrating ESG into a single impact measurement.
- Matching the timeframe of forecasts for risk, return and impact.
For these reasons it is unlikely that pension fund portfolio construction in a 3-D world will become purely systematised any time soon. For 3-D investing to approach systematisation it would require these issues to be addressed while resolving how to set an objective – perhaps utility functions will come to the fore.
Applying some of the outlined portfolio management science will be important: plan members and regulators will at some point want to understand how portfolio trade-offs have been determined. Many of the leading pension funds and asset managers are already well advanced on the technical aspects. But decision-making art will be an important complement to decision-making science.
A final observation is that the role of the portfolio manager will become even more important: portfolio managers will need to understand the range of portfolio outcome possibilities and lead their respective boards through a process for determining an appropriate portfolio. Education and communication remain essential skills.
David Bell is executive director of The Conexus Institute



